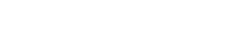脇差　大阪住人月山貞勝謹作（花押） 昭和三年十一月吉日　御即位御大典奉祝為記念　特別保存刀剣鑑定書

品番：WA-120123
価格 (price)1,300,000円(JPY)
（消費税込。10万円以上の商品は国内送料込）

鑑定書：Paper(Certificate): 特別保存刀剣鑑定書

国 Country(Kuni)・時代 Era(Jidai)： 大阪府-奈良県(Osaka-Nara)・昭和三年(Showa era 1928)

刃長：Blade length(Cutting edge): 54.8cm（一尺八寸一分）　反り：Curve(SORI): 1.5cm
元幅：Width at the hamachi(Moto-Haba): 2.73cm　元鎬重：Thickness at the Moto-Kasane: 0.56cm
先幅：Wide at the Kissaki(Saki-Haba): 2.25cm　 先鎬重：Thickness at the Saki-Kasane: 0.50cm
茎：Sword tang(Nakago): 生ぶ、化粧筋違鑢目、目釘孔1個。

体配：Shape(Taihai): 鎬造、庵棟、中切先。
地鉄：Jigane(Hada): 板目肌。
刃文：Temper patterns(Hamon): 互の目乱れ。
帽子：Temper patterns in the point(Bohshi): 湾れて先小丸へ返る。
登録：Registration Card: 東京都

【解説】
月山貞勝は、帝室技芸員（現 人間国宝）である初代貞一の嫡男であり、明治二年（1869）に大阪槍屋町にて生まれる。本名を栄太郎という。幼少より父貞一の元で鍛刀技を修めるが、父の晩年まで相槌を務めて代作を成したため、自身銘の作品は少ない。父の没後、当時の宮相であった一木喜徳郎の知遇を得て、天皇陛下の大元帥刀や皇室御用刀、陸海軍将官の御下賜刀製作を行う栄誉に浴する。指導者としても才を誇り、門下のうち、高橋貞次、貞勝の三男である二代貞一は、両名共に後に人間国宝（重要無形文化財保持者）となっている。同工作風は、師伝の綾杉肌鍛に限らず、各伝に通じ、特に備前伝や相州伝が得意であった。
本刀体配は、刃長が一尺八寸一分と身幅細身ながら長めで、反りがよく利き、雅な小太刀姿を呈する記念刀である。地鉄は、よく鍛錬された板目肌に地沸が付き、荒沸が強く散らされ、精良且つ強靭な鍛肌をみせる。刃文は高低よくついた互の目乱れで、焼頭に荒沸が線状に頻りにかかって、力強い金筋、湯走り風となる。峰に雲が連なるかの如きその様は、同工の力量の程を表して興趣を感ぜられる。帽子は湾れて先小丸へと返る。本作品は昭和天皇の「即位の礼」、その後行われる「大嘗祭」を含む皇室行事（御大典）を記念して製作された入念作。希少性が高く、相伝出来を思わせる覇気のある焼刃は特に見所である。白鞘、金着一重はばき。特別保存刀剣鑑定書。